
A capacitor (originally known as a condenser) is a passive two-terminalelectrical component used to store energy electrostatically in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors (plates) separated by a dielectric (i.e. insulator). The conductors can be thin films, foils or sintered beads of metal or conductive electrolyte, etc. The "nonconducting" dielectric acts to increase the capacitor's charge capacity. A dielectric can be glass, ceramic, plastic film, air, vacuum, paper, mica, oxide layer etc. Capacitors are widely used as parts of electrical circuits in many common electrical devices. Unlike a resistor, an ideal capacitor does not dissipate energy. Instead, a capacitor stores energy in the form of an electrostatic field between its plates.
When there is a potential difference across the conductors (e.g., when a capacitor is attached across a battery), an electric field develops across the dielectric, causing positive charge +Q to collect on one plate and negative charge −Q to collect on the other plate. If a battery has been attached to a capacitor for a sufficient amount of time, no current can flow through the capacitor. However, if a time-varying voltage is applied across the leads of the capacitor, a displacement current can flow.
An ideal capacitor is characterized by a single constant value for its capacitance. Capacitance is expressed as the ratio of the electric charge Q on each conductor to the potential difference V between them. The SI unit of capacitance is the farad (F), which is equal to one coulomb per volt (1 C/V). Typical capacitance values range from about 1 pF (10−12 F) to about 1 mF (10−3 F).
The capacitance is greater when there is a narrower separation between conductors and when the conductors have a larger surface area. In practice, the dielectric between the plates passes a small amount of leakage current and also has an electric field strength limit, known as the breakdown voltage. The conductors and leadsintroduce an undesired inductance and resistance.
Capacitors are widely used in electronic circuits for blocking direct current while allowing alternating current to pass. In analog filter networks, they smooth the output of power supplies. In resonant circuits they tune radios to particular frequencies. Inelectric power transmission systems, they stabilize voltage and power flow.

Theory of operation:
A capacitor consists of two conductorsseparated by a non-conductive region.The non-conductive region is called thedielectric. In simpler terms, the dielectric is just an electrical insulator. Examples of dielectric media are glass, air, paper,vacuum, and even a semiconductor depletion region chemically identical to the conductors.
A capacitor is assumed to be self-contained and isolated, with no net electric charge and no influence from any external electric field. The conductors thus hold equal and opposite charges on their facing surfaces and the dielectric develops an electric field. In SIunits, a capacitance of one farad means that one coulomb of charge on each conductor causes a voltage of one volt across the device.
An ideal capacitor is wholly characterized by a constant capacitance C, defined as the ratio of charge ±Q on each conductor to the voltage V between them:
Because the conductors (or plates) are close together, the opposite charges on the conductors attract one another due to their electric fields, allowing the capacitor to store more charge for a given voltage than if the conductors were separated, giving the capacitor a large capacitance.
Networks:
- For capacitors in parallel
- Capacitors in a parallel configuration each have the same applied voltage. Their capacitances add up. Charge is apportioned among them by size. Using the schematic diagram to visualize parallel plates, it is apparent that each capacitor contributes to the total surface area.
- For capacitors in series
- Connected in series, the schematic diagram reveals that the separation distance, not the plate area, adds up. The capacitors each store instantaneous charge build-up equal to that of every other capacitor in the series. The total voltage difference from end to end is apportioned to each capacitor according to the inverse of its capacitance. The entire series acts as a capacitor smaller than any of its components.
- Capacitors are combined in series to achieve a higher working voltage, for example for smoothing a high voltage power supply. The voltage ratings, which are based on plate separation, add up, if capacitance and leakage currents for each capacitor are identical. In such an application, on occasion, series strings are connected in parallel, forming a matrix. The goal is to maximize the energy storage of the network without overloading any capacitor. For high-energy storage with capacitors in series, some safety considerations must be applied to ensure one capacitor failing and leaking current will not apply too much voltage to the other series capacitors.
- Series connection is also sometimes used to adapt polarized electrolytic capacitors for bipolar AC use.
Parallel-plate model:
- Dielectric is placed between two conducting plates, each of area A and with a separation of d
Non-ideal behavior:
- Capacitors deviate from the ideal capacitor equation in a number of ways. Some of these, such as leakage current and parasitic effects are linear, or can be assumed to be linear, and can be dealt with by adding virtual components to theequivalent circuit of the capacitor. The usual methods of network analysis can then be applied. In other cases, such as with breakdown voltage, the effect is non-linear and normal (i.e., linear) network analysis cannot be used, the effect must be dealt with separately. There is yet another group, which may be linear but invalidate the assumption in the analysis that capacitance is a constant. Such an example is temperature dependence. Finally, combined parasitic effects such as inherent inductance, resistance, or dielectric losses can exhibit non-uniform behavior at variable frequencies of operation.
Q factor:
- The quality factor (or Q) of a capacitor is the ratio of its reactance to its resistance at a given frequency, and is a measure of its efficiency. The higher the Q factor of the capacitor, the closer it approaches the behavior of an ideal, lossless, capacitor.The Q factor of a capacitor can be found through the following formula:where
is angular frequency,
is the capacitance,
is the capacitive reactance, and
is the series resistance of the capacitor.
Applications:
- Energy storage
- Pulsed power and weapons
- Power conditioning
- Power factor correction
- High pass and low pass filter
- Noise suppression, spikes, and snubbers
- Motor starters
- Oscillators

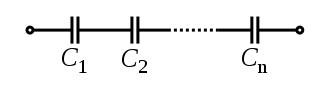

Comments
Post a Comment